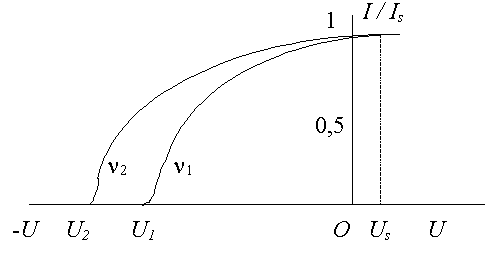
ЗАКОНОМЕРНОСТИ ФОТОЭФФЕКТА В КЛАССИЧЕСКОЙ СТАТИСТИЧЕСКОЙ ФИЗИКЕ  

   При попытках объяснить фотоэффект, как правило, в ВУЗовских учебниках допускаются довольно грубые ошибки. Так, например, утверждается, что, якобы, согласно Классической физике при увеличении интенсивности падающего на фотокатод света должна увеличиваться энергия вылетающих фотоэлектронов, чего на самом деле не происходит. Увеличивается лишь общее количество вылетающих фотоэлектронов, а распределение электронов по скоростям и энергиям остается прежним и не зависит от величины потока падающего на фотокатод света. И, как результат подобных заблуждений, начинается выдумывание разных "квантовых диковинок" типа фотонов как некоторых сгустков энергии, которые, якобы, и бьют метко по электронам, выбивая их наружу. При первом же детальном анализе явления фотоэффекта подобные "истолкования" не выдерживают элементарной критики.

   Сразу же следует сказать, что изобретатели "новых теорий", просто-напросто, не учитывают статистический характер света.

   Статистический характер световых полей обусловлен тем, что источники света обычно состоят из огромного числа хаотически расположенных в пространстве и не связанных между собой элементарных излучателей (атомы, молекулы), испускание света которыми имеет вероятностный характер [1]. Поэтому рассмотрение данной задачи следует вести исключительно в рамках статистической физики и статистической оптики с использованием функций распределения электронов по скоростям или по энергиям.

  Рассмотрение этого сложного вопроса начнем с анализа энергетического распределения (функции распределения) фотоэлектронов, возникающих при облучении фотокатода светом определенного спектрального состава.

   Распределение фотоэлектронов по энергиям обычно исследуют методом задерживающего потенциала в сферическом вакуумном диоде с центральным фотокатодом. Вольт-амперные характеристики сферического диода, измеренные при освещении центрального катода светом различных частот, представлены на рис. 1.    

   Полный сбор фотоэлектронов (ток насыщения  I_s ) достигается при некотором положительном напряжении на аноде   U_s.  При подаче на коллектор отрицательного тормозящего напряжения    -U   на него попадут только те фотоэлектроны, начальная энергия которых достаточна для преодоления тормозящего поля, т.е.    mv²/2  >  eU.   При величине задерживающего потенциала, соответствующего кинетической энергии самого быстрого фотоэлектрона, ток в цепи коллектора обращается в нуль.

   Распределение фотоэлектронов по начальным кинетическим энергиям   dn/dE  получается дифференцированием вольт-амперных характеристик (рис. 1).   Форма функции распределения фотоэлектронов по энергиям напоминает максвелловское распределение частиц по скоростям, однако, имеется ограничение со стороны максимальных значений кинетической энергии фотоэлектронов  E_m, которая определяется частотой падающего света, (Рис. 2).  

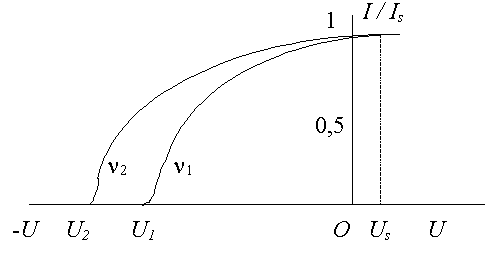
Рис. 1. Вольт-амперные характеристики вакуумного фотоэлемента для двух частот падающего на фотокатод света

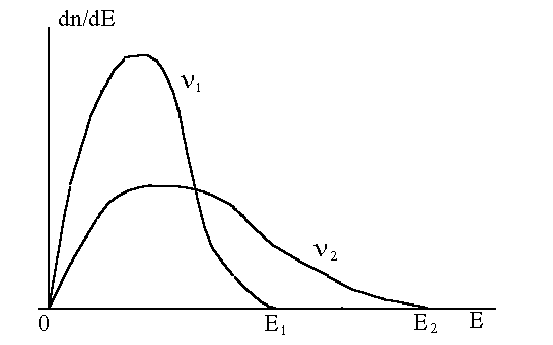
 Рис. 2. Энергетическое распределение фотоэлектронов для двух частот падающего на фотокатод света

   Отметим характерную особенность данных кривых. Хотя облучение фотокатода производится почти монохроматическим светом, распределение фотоэлектронов по энергиям имеет непрерывный характер, как и в случае термоэмиссии. Таким образом, мы имеем дело со статистическим процессом взаимодействия электромагнитных волн с электронной плазмой фотокатода.

   Из статистической физики известно, что при достаточно большом числе участвующих в процессе частиц форма функции распределения не зависит от количества частиц, а определяется другими факторами. 

   Функция распределения фотоэлектронов по энергиям есть функция отклика электронной плазмы фотокатода на статистическое поле падающих световых волн, которое формируется благодаря огромному числу излучающих атомов. Так как фазы и направления поляризации излучения каждого атома являются случайными, то в результате сложения огромного числа независимых волн образуется некоторое распределение статистического волнового поля по амплитудам и фазам векторов   Е   и   Н.

   Как и для многих других распределений, функция распределения по амплитудам для статистического электромагнитного поля не должна зависеть от количества участвующих в процессе излучения атомов. Подобные свойства световых полей рассматриваются в статистической оптике и статистической радиофизике [1-2].

   На рис. 1 приведены нормированные на единицу кривые фототока. В общем случае величина фототока зависит как от величины полного светового потока    Ф,  так и от его спектрального состава. Поэтому характеристика фототока является функцией двух параметров светового потока:   Ф  и    n, т.е.   I =  I ( Ф ,n ).

   Предположим, что мы работаем с монохроматическим светом. Если мы увеличим в два раза световой поток    Ф,  то это приведет просто к двукратному увеличению фототока   I.  При этом форма вольт-амперной характеристики останется неизменной, поскольку вид функции распределения световых волн по амплитудам, а следовательно, и функции распределения электронов по энергиям не зависят от числа участвующих частиц, т.е. от величины светового потока    Ф. Такое свойство светового потока соответствует принципу суперпозиции, и оно присуще только для статистических волн, но не для волн, генерируемых одной антенной, что очень часто путают в ВУЗовских учебниках при описании явления фотоэффекта.

   Таким образом, мы получили, что величина фототока пропорциональна световому потоку для одного и того же спектрального состава света, и его можно выразить в виде соотношения

I = Ф f ( n ),                                    (3.68)

где    f (n)  - некоторая функция частоты падающего света, определяющая

также и форму вольт-амперной характеристики   I (U).

   Теперь увеличим расстояние между источником света и фотоэлементом таким образом, чтобы световой поток, достигающий фотокатода, уменьшился в два раза. Восстановить величину светового потока  Ф,  а следовательно, и фототок до прежнего уровня можно, просто добавив еще один точно такой же источник света. Вполне естественно, что от двух одинаковых источников света форма вольт-амперной характеристики не должна измениться, поскольку вид функций распределения  волн по амплитудам для светового поля и, следовательно, функция распределения электронов по энергиям не должны зависеть от числа излучающих атомов в источниках света.

   Итак, мы приходим к очень важному выводу: форма нормированной вольт-амперной характеристики фотоэлемента, а следовательно, и функция распределения фотоэлектронов по энергиям для статистических волн не зависят от величины светового потока   Ф  и от расстояния до источника света, а определяются только спектральным составом излучения. Другими словами, масштаб энергии для фотоэлектронов определяется только частотой источника света, состоящего из огромного числа независимых излучателей - атомов.

   Детальные исследования  показали, что в общем случае распределение фотоэлектронов по энергиям зависит от материала и толщины фотокатода  [3], однако это связано, в первую очередь, с работой выхода и с энергетическими потерями фотоэлектронов при их выходе на поверхность из глубины фотокатода.

   Для очень тонких (пленочных) металлических фотокатодов вид функций распределения фотоэлектронов по энергиям является более простым и определяется, в основном, работой выхода фотоэлектрона из металла в вакуум.

   После установления свойств функции распределения фотоэлектронов по энергиям осталось определить граничную энергию    E_m (рис. 2) как функцию частоты света   n. Пользуясь тем замечательным свойством, что функция энергетического распределения фотоэлектронов не зависит от расстояния между источником света и фотокатодом, приблизим источник света к фотокатоду настолько, чтобы существовала конечная вероятность передачи всей энергии излучения от отдельного излучающего атома одному фотоэлектрону. В параграфе 47  работы [4] было отмечено, что энергия  Е,   которую может излучить электрон в атоме, связана со средней разностной частотой   n  движения электрона в атоме между двумя энергетическими уровнями посредством соотношения   E = hn.  Следовательно,    hn   является максимально возможным значением энергии, которую может передать излучающий электрон в атоме отдельному фотоэлектрону.

   Поскольку вероятность этой передачи ничтожно мала, то функция распределения фотоэлектронов по энергиям    dn/dE   в точке    E_m = hn    должна обратиться в нуль. Обычно такая граничная точка на оси энергий определяется методом экстраполяции вольт-амперной характеристики к нулевому значению величины фототока.

   Таким образом, мы установили, что благодаря статистическому характеру взаимодействия электронов фотокатода с электромагнитными полями граничная энергия    E_m   в функции распределения фотоэлектронов по энергиям   dn/dE  (рис. 2)   не зависит от интенсивности света и расстояния между источником света и фотокатодом, а определяется только разностной частотой    n,   на которой происходит излучение света атомами, и работой выхода электронов из фотокатода.

   Вполне понятно, что благодаря наличию этой работы выхода существует граничная частота   n_min - красная граница фотоэффекта, ниже которой фотоэффект невозможен, поскольку фотоэлектроны, обладая энергиями ниже энергетического барьера при выходе в вакуум, не могут выйти за пределы фотокатода.

   Внешне явление фотоэффекта напоминает рассеяние некоторых сгустков энергии    hn    подобно частицам на электронах фотокатода, что и побудило физиков ввести некие гипотетические частицы, названные фотонами и обладающие данной энергией    hn.  Теперь же мы видим, что эта гипотеза очень далека от реальных статистических процессов обмена энергией между электронами и статистическим полем электромагнитных волн со случайным распределением по амплитудам  и фазам напряженностей     Е   и   Н.

   На примере рассмотрения фотоэффекта в рамках Классической статистической физики хорошо видно, что и все остальные задачи, связанные с взаимодействием излучения с веществом, следует решать статистическими методами.

  ЛИТЕРАТУРА

1. Физический энциклопедический словарь / Ред. Прохоров А.М. – М.: Сов. энциклопедия, 1984. С. 718.

  2. Ахманов С.А., Дьяков Ю.Е., Чиркин А.С. Введение в статистическую  радиофизику и оптику. М.: Наука, 1981.

3. Соболева Н.А., Меламид А.Е. Фотоэлектронные приборы. М.: Высшая школа, 1974. C. 58.  

4. Шаляпин А.Л., Стукалов В.И. Введение в классическую электродинамику и атомную физику. Второе издание, переработанное и дополненное. Екатеринбург, Изд-во  Учебно-метод. Центр УПИ, 2006, 490 с.

За дополнительной информацией можно обратиться на сайты: 

http://s6767.narod.ru  http://s1836.land.ru  http://s1836.narod.ru

  http://shal-14.boom.ru  http://shal-14.narod.ru