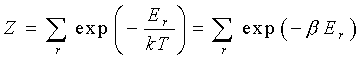НАИБОЛЕЕ ТИПИЧНЫЕ ОШИБКИ, ДОПУСКАЕМЫЕ В КВАЗИСОВРЕМЕННОЙ АБСТРАКТНОЙ ФИЗИКЕ – 4

 О КЛАССИЧЕСКОМ СМЫСЛЕ КВАНТОВОЙ МЕХАНИКИ И ЕЕ МЕСТЕ В ЕДИНОЙ ФУНДАМЕНТАЛЬНОЙ ФИЗИКЕ

   По причине несовершенства наших измерительных приборов в атомной физике были получены необычные экспериментальные результаты, которые не укладывались в привычных представлениях физиков начала ХХ века. На этой основе была построена специальная вероятностная математическая теория – квантовая механика, способствующая расчету полученных экспериментальных результатов, а также предсказанию новых.

   В первое время смысл этого математического аппарата был совершенно не понят физиками. Однако в дальнейшем появились некоторые просветы, а вместе с ними и надежда на понимание смысла квантовой механики и ее математического аппарата с волнами де Бройля или пси-функциями.

   Появление квантовой механики в начале ХХ века стимулировало огромный поток дискуссий по поводу природы микрочастиц и силовых полей.

   Явления, которые наблюдались в микромире, были столь необычными, что микрочастицам был приписан особый статус квантовых явлений, в корне отличающихся от явлений, происходящих в привычной для всех классической физике.

   В этом новом мире микрочастиц странности встречаются буквально на каждом шагу. С одной стороны, все микрочастицы совместно с электромагнитными волнами аккуратно соблюдают все законы сохранения классической механики Ньютона, как бы намекая на то, что все они, в общем-то, «ребята неплохие», и их, в принципе, при желании вполне можно понять.

   С другой стороны, и микрочастицы, и электромагнитные волны в атомных явлениях «откалывали» такие квантовые «номера», что привели в замешательство весь научный мир.

   Так, в чем же здесь дело? Попробуем постепенно в этом разобраться.

   Прежде всего, что касается самих экспериментов в микромире. Авторы квантовой теории почему-то решили, что наши измерительные приборы являются идеальными, а все «фокусы» в экспериментах обусловлены исключительно особой природой микрочастиц. Здесь явно содержится логическая ошибка. По их представлению, оказывается виноваты не измерительные приборы с их несовершенством и даже некоторой грубостью, а все дело в особых, неуловимых, «квантовых» свойствах самих микрообъектов, которые никак не поддаются измерению.

   Здесь мы имеем яркий пример того, когда пытаются, как говорится, переложить вину с больной головы на здоровую. Неужели хотя бы часть вины за квантовые «чудеса» нельзя переложить на измерительные приборы? Может быть, как раз все наоборот: микрочастицы – самые, что ни есть, классические объекты, а вот с помощью несовершенных приборов мы и выявляем различные квантовые закономерности. И это подозрение не лишено обоснования.

    Обычные лабораторные приборы способны измерять лишь средние значения физических величин. Их в физике назвали «наблюдаемые» величины. При этом усреднение происходит, как правило, по большому числу частиц и по времени. Этот процесс называется набором статистики в эксперименте. Следовательно, в наших экспериментах мы как раз и получаем статистические закономерности в микромире, а отнюдь не характеристики отдельных микрочастиц.

   С легкой руки теоретиков, эти статистические, квантовые закономерности были перенесены на отдельную микрочастицу и, в частности, на электрон. Это совершенно неправомерно, поскольку у нас даже нет в наличии такого прибора, чтобы тщательно проследить за полетом отдельного электрона в атоме. Так начинает выстраиваться «квантовая квазифизика», не отражающая реальных индивидуальных свойств отдельных микрочастиц.

   Какой же выход из всей этой ситуации? Прежде всего, стараться не смешивать статистические закономерности в микромире, которые выявляются в экспериментах, с индивидуальными свойствами отдельных микрочастиц. Далее здравый смысл подсказывает, что следует просто вернуться в классическую статистическую физику с ее функциями распределения физических величин и постараться здесь разрешить все проблемы с микрочастицами и электромагнитными волнами.

   Теперь попытаемся раскрыть основные секреты квантовой механики, которые до недавнего времени воспринимались не иначе, как тайна за семью печатями.

   Принцип неопределенностей Гейзенберга, который был постулирован им на основе экспериментальных наблюдений и на основе постулированного математического аппарата квантовой механики, в статистической физике, вполне естественным образом, следует из центральной теоремы Лиувилля о сохранении фазового объема системы частиц [1]. Исходя из этой теоремы, а также с привлечением спектрального метода Фурье, строится и весь математический аппарат квантовой механики.

   Далее выяснилось, что так называемые «корпускулярно-волновые» свойства частиц вещества - это просто всего-навсего непонятое физическое явление. А разгадка его не так уж и сложна. Секрет заключается в дискретном отклике монокристалла на любую налетающую частицу. В эксперименте нам кажется, что таким "хитрым" способом ведет себя частица, а на самом деле это всего лишь определенная реакция подложки на частицу.

   В частности, у монокристалла имеет место дискретный спектр распределения электронов по импульсам, что хорошо известно в физике твердого тела и в квантовой механике. Поэтому и реакция кристалла на микрочастицу, независимо от ее природы, является дискретной, т.е. в виде отдельных пиков.

   При дифракции электронов даже на двух щелях и даже поодиночке падающие электроны повторяют функцию распределения электронов вещества в экране.

   Это - самая «хитрая» задача, на которой споткнулся весь мир. А разгадка - довольно простая. Электроны своими электрическими полями взаимодействуют с электронами экрана и приобретают функцию распределения электронов экрана. То есть, как бы «прогреваются» от экрана. А функция распределения электронов экрана находится методом Фурье.

   Вот и получается такая красивая картинка с волнами согласно преобразованию Фурье. В квантовой механике нет орбит, как нет их и в классической статистической физике, и даже в молекулярной физике.

   У электронов же орбиты имеются, и еще никто не доказал, что у электронов нет орбит. У нас нет таких приборов, которые отслеживали бы орбиты медленных электронов. Но быстрые электроны наблюдаются очень хорошо.

   Посылая электроны по одному, но достаточно долго, мы, в конце концов, создадим ту же самую интерференционную картину, как и для пучка электронов. Этот случай полностью соответствует эргодической гипотезе (а может быть и теореме) в классической статистической физике.

   Кратко она выглядит так: если взять среднее по ансамблю частиц (мгновенный снимок) или усреднить результат по времени (метод накопления информации во времени), то результат будет одним и тем же в силу статистической независимости событий. Это означает, что каждый электрон не должен знать о прохождении других электронов. В противном случае появятся различные тонкие эффекты, которых в физике просто огромное количество.

   Известен эффект дифракции электронов на границе пластинки, а также на отдельной проволочке [2]. Но суть задачи не меняется - решение то же самое. Проволочка разлагается в интеграл Фурье, и получаем соответствующую функцию распределения электронов по импульсам в проволочке. Налетающие электроны повторят функцию распределения по импульсам электронов проволочки или пластинки, в результате чего и получается соответствующая дифракционная картина, полностью соответствующая преобразованию Фурье.

   Итак, мы приходим к очень важному выводу, что квантовая механика вместе с волнами де Бройля и прочими постулатами - это самая обычная классическая статистическая физика микромира с функциями распределения физических величин, но с применением хорошо развитого спектрального метода Фурье. Волновая функция в квантовой механике, она же - собственная функция при решении уравнения на собственные значения в краевой задаче, она же - волна де Бройля неизвестного происхождения и не имеющая никакого физического смысла, она же компонента Фурье при разложении произвольной функции в ряд или интеграл Фурье. По модулю в квадрате эта пси-функция дает нам обычную функцию распределения электронной плотности или плотность вероятности, так хорошо известную еще в Х1Х веке. Может быть, настало время все-таки определиться с этой волной?

   Хорошо известно, что операторные методы решения дифференциальных уравнений в различных разделах физики и техники возникли в результате применения спектрального метода Фурье. Поэтому неудивительно, что и в квантовой механике оператор импульса, а также и другие операторы возникли как результат применения спектрального метода Фурье для функций распределения физических величин.

   Такие функции распределения были известны еще с ХIХ века (функция распределения по скоростям Максвелла для молекул газа и функция распределения по координатам молекул газа в гравитационном поле – барометрическая формула Больцмана, функции распределения Гиббса и т.д.). Вот, в правильном использовании и понимании спектрального метода Фурье применительно к функциям распределения физических величин и возникли наибольшие трудности практически у всех физиков.

   Основоположникам статистической физики не приходило в голову представлять отдельную молекулу или атом в виде размытого облака по всему объему сосуда, а также особенно печалиться о неопределенности положения молекулы газа внутри сосуда. Не очень заботило их и то, что в статистической физике с траекториями частиц вполне естественным образом просто придется распрощаться. Однако и Максвелл, и Больцман, и Гиббс, прекрасно осознавали, что траектории частиц продолжают существовать, хотя эти траектории и выпали из рассмотрения в статистической физике. Они воспринимали случайность в микромире, где в процессах участвует огромное количество микрочастиц, как вполне объективную закономерность. Все эти проблемы в физике микромира были искусственно придуманы авторами квантовой теории, благодаря чему и был искусственно спровоцирован квазикризис в физике в начале ХХ века.

§ 30. Функции распределения электронной плотности в Фурье-представлении

    С целью успешного применения статистических методов описания электронных процессов, происходящих в атомах, вспомним некоторые моменты из статистической физики.

   При статистическом описании состояние системы изображается точкой в соответствующем фазовом пространстве (фазовая точка с координатами  p  и q). Изменение состояния системы изображается траекторией фазовой точки в фазовом пространстве – фазовой траекторией.

   Благодаря использованию фазового пространства законы изменения состояния системы могут быть сформулированы на геометрическом языке.

   Основным положением статистической физики является утверждение о возможности определить функцию распределения (или плотность вероятности состояний) w(p,q) из общих соображений, в том числе и из геометрических для систем, находящихся в состоянии термодинамического равновесия, т.е. не решая уравнений движения для отдельных частиц.

   Согласно теореме Лиувилля [3] функция распределения является интегралом движения системы, т.е. остается постоянной, если импульсы p и координаты q изменяются в соответствии с уравнениями движения механики Гамильтона, т.е. каноническими уравнениями. При этом фазовый объем системы (объем в переменных p и q) в результате ее естественного движения остается постоянным. Это свойство можно выразить при помощи интеграла

∫ d Г =  ∫  d p d q = const,                            (30.1)

где  d Г  обозначает элемент объема фазового пространства.

   Рассмотрим наиболее общие свойства функции распределения w. В статистической механике для полного описания состояния движения частицы достаточно указать вероятность, с которой координата частицы лежит в области от q  до  q + dq,  и одновременно ее импульс – в интервале от  p до  p + dp, т.е. в некотором элементе объема фазового пространства d p d q, или в декартовых координатах –  dx dy dz dp_x dp_y dp _z.

   В случае стационарных процессов, когда система частиц находится в термодинамическом равновесии и в стационарном  состоянии, возможно использование стационарной функции распределения только по координатам w(x, y, z). Принимая во внимание тот факт, что функция распределения по своей величине является принципиально неотрицательной, т.е. w(x, y, z) ³ 0, ее можно  выразить в комплексном пространстве через вспомогательную комплексную функцию (комплексную амплитуду) Ф(x, y, z) посредством выражения

Ф(x, y, z) = |Ф(x, y, z)| ² = Ф*Ф.                 (30.2)

   С использованием функции распределения w(x, y, z) средняя потенциальная энергия электрона по области его движения определяется через объемный интеграл

<U> = ∫ U(x, y, z) w(x, y, z) dV                  (30.3)

или, с учетом выражения (30.2),

<U> = ∫ Ф*UФ dV.                                    (30.4)

  Функция распределения, как правило, нормируется посредством интеграла

∫  w(x, y, z) dV  = ∫ Ф*Ф dV = 1.                   (30.5)

   Таким образом, задача на нахождение функции  распределения электронной плотности w(x, y, z) в атомах сводится к отысканию некоторой комплексной характеристической функции Ф(x, y, z), через которую могут быть определены не только плотность вероятности местопребывания электронов в атомах, но также и, как будет показано в дальнейшем, целый ряд интегралов движения. С целью вычисления функции Ф(x, y, z) необходимо составить для нее дифференциальное уравнение, максимально используя при этом всю известную нам заранее информацию об атомах. Для этого можно воспользоваться известными из классической механики законами сохранения определенных динамических величин (например, полной энергии   Е,  модуля полного механического момента   L,  а также проекции механического момента на ось симметрии атома   L_z ).

 О КЛАССИЧЕСКОМ КВАНТОВАНИИ УРОВНЕЙ ЭНЕРГИИ В АТОМАХ

    В современной физике сложилось упрощенное схематическое (модельное) представление о квантовых переходах-прыжках электронов между дискретными уровнями энергии в атомах и молекулах на основе опытов, когда были обнаружены линейчатые спектры излучения ряда веществ. Возможно, что очень похожие процессы происходят и в ядрах. Попытаемся разобраться в этом более детально, опираясь на богатый накопленный опыт в спектроскопии и исходя из классических представлений в рамках электродинамики Максвелла-Лоренца.

   Квантование по энергии, а точнее формирование дискретных уровней энергии в атомах происходит в соответствии со стационарным статистическим уравнением Шредингера, т.е. в стационарном состоянии атомной системы или в веществе, когда все переходные процессы в основном уже закончены.

   На опыте достаточно узкие спектральные линии излучения или поглощения наблюдаются в охлажденных кристаллах, активированных переходными элементами таблицы Менделеева, в слабо возбужденных холодных газах и т.д. В охлажденных системах и при отсутствии больших внешних возмущений у системы атомов имеется достаточно времени, чтобы прийти в равновесное состояние и сформировать дискретные энергетические уровни.

   Однако эти уровни могут значительно ушириться и даже вообще исчезнуть в сильно нагретых кристаллах и газах. В этом случае всякое квантование уровней энергии может полностью отсутствовать, и вещество будет излучать в сплошном спектре частот, напоминающем спектр излучения абсолютно черного тела.

   В качестве примера достаточно привести поведение ртутной газоразрядной лампы низкого давления. При малом разрядном токе и холодных парах ртути спектр излучения такой лампы состоит из очень узких характерных линий. Однако по мере прогрева лампы и повышения давления паров ртути происходит значительное уширение данных линий. В ртутных лампах сверхвысокого давления при высокой температуре лампы ее спектр свечения является сплошным и приближается к спектру излучения абсолютно черного тела, а наиболее яркие ртутные линии превращаются в полосы свечения. Это происходит из-за того, что в результате очень частых столкновений атомов между собой уровни энергии электронных оболочек не успевают проквантоваться, что опровергает гипотезу обязательного квантования уровней энергии в атомах.

   Дипольное излучение света в системе атомов происходит на разностных средних частотах движений электронов в оболочках, т.е. на частотах биений электронной плотности, если это не запрещено правилами отбора для дипольного излучения в данных электронных конфигурациях. При этом энергия для излучения атомов черпается из кулоновского поля ядер при переходе электронов с более удаленных орбит на орбиты, расположенные ближе к ядру.

   Таким образом, в процессе излучения света атомами можно выделить два характерных явления, которые становятся как бы взаимоисключающими. С одной стороны, при малых возмущениях атомы стремятся выстроить дискретные уровни энергии в своих электронных оболочках в полном соответствии со статистическим уравнением Шредингера для функций распределения электронной плотности в атомах. С другой же стороны, эта дискретная система уровней постепенно разрушается за счет потери энергии на излучение.

   Согласно выводам классической электродинамики, потеря энергии на излучения электронами на атомных орбитах происходит достаточно медленно - с добротностью осцилляторов около 10⁷. В таких условиях у атомов имеется достаточно времени для формирования узких дискретных уровней энергии. Поэтому в холодных газах уширение уровней энергии, а, следовательно, и спектральных линий происходит, в основном, за счет конечного радиационного времени жизни возбужденных электронов на данных уровнях. Подобное уширение спектральных линий называется радиационным уширением.

   Весь набор опытных данных в спектроскопии говорит о том, что как излучение, так и поглощение электромагнитных волн в атомных системах не является результатом некоторых квантовых прыжков электронов с уровня на уровень, а происходит по обычным законам классической электродинамики, но с учетом статистических закономерностей в сложных системах. Так называемые “квантовые эффекты” и другие дискретные закономерности в оптических спектрах появляются в сложных атомных системах в соответствии с законами классической статистической физики [1].

 Особенности статистической физики в классическом и квантовом представлении

    Для определения основных характеристик сложной атомной системы в современной физике используется статистическая сумма в роли своеобразной производящей функции [4]

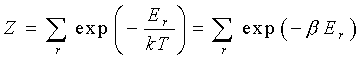  .              (1)

   При этом сразу же предполагается, что энергия E_r в системе является дискретной переменной, т.е. является счетной величиной, а статистическая сумма вида (1) относится исключительно к квантовой механике. Одновременно с этим рассматривается квантовое состояние r  системы или частицы с дискретной энергией E_r, а также вероятность P_r   нахождения частицы в этом состоянии

  ,                                   (2)

 где C – коэффициент пропорциональности, равный 1 / Z; E_r  – уровни энергии электронов, атомов, или молекул в системе.

   Введение дискретных состояний энергии системы было впервые осуществлено М. Планком в начале ХХ века и с тех пор прочно обосновалось в современной физике.

   Наряду со статистической суммой Z в современной физике используется такое понятие как статистический вес Ω(E) состояния или число способов, которыми может быть реализована данная макроскопическая конфигурация.

   Энтропия системы, определяемая по Планку как

  ,                                      (3)

 в ином представлении, кроме квантового, даже не рассматривается.

   Действительно, бросается в глаза то, что счетные состояния системы принято рассматривать исключительно лишь в квантовой механике, не взирая на то, что сами электроны, атомы и молекулы являются счетными объектами. Поэтому согласно классической статистике Больцмана эти объекты могут с полным успехом участвовать в счетной комбинаторике без введения каких-либо искусственных квантовых постулатов. В этом, на наш взгляд, заключается логическое противоречие в подходе Планка.

   В некоторых академических изданиях и учебниках по квантовой статистической физике можно встретить такого рода пассажи [4]: «любая макроскопическая система может быть описана с помощью набора  f  квантовых чисел. Число  f  носит название числа степеней свободы системы, и по порядку величины оно близко к постоянной Авогадро». Но ведь это же просто число частиц в сложной системе, а число f – число проекций обобщенных координат или обобщенных импульсов в фазовом пространстве.

   Таким образом, мы убеждаемся, что квантовые и классические представления смешиваются в одном месте без достаточного анализа и обоснования. Кроме этого, заметим, что формула (2) является универсальной в статистике Максвелла-Больцмана и справедлива для любой энергии E атома или молекулы вне зависимости ее от непрерывного или дискретного характера. По этой причине обратимся за разъяснениями к классической физике.

   В классической статистической физике, рассматривающей отдельные атомы или молекулы, движущиеся в силовых полях, статистическая сумма имеет точно такой же вид, как в формуле (1)

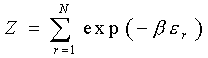  ,                               (4)

где ε_r – полная энергия молекулы под номером r, и суммирование осуществляется по всем N молекулам. В данном случае параметр r – не квантовое состояние системы, а просто порядковый номер молекулы или атома. Это находится в полном соответствии со статистикой Максвелла – Больцмана. При этом ε_r  может быть просто любой кинетической энергией свободно летящей молекулы в газе. Эта энергия по своему характеру может быть как непрерывной, так и дискретной величиной. Заметим, что согласно подходу Планка энергия ε_r  должна быть непременно дискретной, т.е. квантованной величиной, а суммирование должно производиться по квантовым состояниям   r  атома, молекулы или какой-либо системы.

   Следует также отметить, что сложную макроскопическую систему можно разбить на отдельные подсистемы, пронумеровать их и производить по ним суммирование как по счетным объектам, т.е. без какого-либо искусственного квантования.

   Таким образом, мы видим, что классическая физика охватывает больший круг явлений микромира, чем квантовая механика. При этом средняя энергия атома или молекулы в классической физике определяется в соответствии с обычной формулой статистической физики

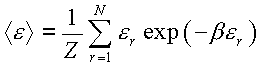  ,                         (5)

т.е. не требует введения какого-либо особого квантования. Ведь сами объекты – атомы и молекулы уже являются дискретными и счетными, поэтому непосредственно могут быть использованы в любой счетной комбинаторике.

   Основная ошибка квантовой статистики заключается в следующем: динамические переменные q и p принимают непрерывные значения, но требуется вопреки всему найти способ сделать возможные состояния системы счетными. Для этого область изменения переменных q и p в фазовом пространстве искусственно разбивается на малые дискретные интервалы, т.е. элементарные ячейки. Без строгого обоснования размер элементарной ячейки приравнивается постоянной Планка h. Теперь для квантового описания состояния частицы указывают, что пара переменных  (q, p) лежит в некотором определенном интервале или ячейке дискретного фазового пространства. При этом становится непонятным, почему фазовое пространство атомов или молекул, сравнительно свободно летающих в некотором объеме, должно быть дискретным.

   Квантование фазового пространства было введено Планком в 1900г. как вынужденная мера при выводе формулы для спектра излучения абсолютно черного тела и было принято за основу в качестве главного постулата квантовой теории. Позднее, однако, выяснилось, что вводить такое искусственное квантование вовсе не требуется для решения указанной задачи, что было доказано Эйнштейном на языке вероятностей переходов между произвольными энергетическими уровнями излучающей системы.

   В соответствии с представлениями Больцмана энтропия  S  является мерой хаоса макроскопической системы, и она применима для описания любых систем, а не только квантовых. Согласно Планку энтропия вводится с помощью классической комбинаторики Больцмана, но обязательно через квантование, и последнее уже оказывается проявлением непоследовательности в квантовой теории. Естественно, что с квантовыми числами формально намного проще работать, поэтому они и были выбраны (можно сказать, приняты “на ура!”) в качестве методической основы всех расчетов в ущерб пониманию реально происходящих в природе процессов.

ЗАГАДКА ФУНДАМЕНТАЛЬНОЙ КОНСТАНТЫ ФИЗИКИ – ПОСТОЯННОЙ ПЛАНКА

   На протяжении ХХ века физики ломали голову над тем: чем обусловлена величина постоянной Планка  h  или постоянной тонкой структуры  a. Какова природа  h? Или это квант действия  DS ,  введенный Планком в атомную физику, или механический момент  L  в атомах, который следует из уравнения Шредингера, или величина, определяющая длину волны де Бройля  h/mv, или величина, определяющая импульс электрона  ћ k  в кристаллах, или спин элементарных частиц  s ,  кратный  ћ/2, или минимальный фазовый объем  DW в статистической физике микромира и т.д. ? Вопросов накопилось, как мы видим, немало. Попытаемся в этом разобраться.

   В соответствии с теоремой Лиувилля постоянная Планка  h  может действительно претендовать на минимально возможный фазовый объем для функции распределения электронов по координатам и импульсам в самых разнообразных прикладных задачах. В декартовых координатах элементарный фазовый объем  DW  выглядит так:

                            DW = Dp_x Dp_y Dp_z  Dx D yDz,                      (1)

при этом проекции импульсов  p_x, p_y, p_z  и координаты частицы  x,y,z  рассматриваются как независимые динамические переменные.

   Как же смог сформироваться в природе такой минимальный фазовый объем, который не может обратиться в нуль? Чтобы это понять, необходимо учесть стохастический характер движения электронов в эфире, атомах, молекулах и т.д. Свободные электроны не просто летят по прямым траекториям, а постоянно подвержены воздействию электромагнитных флуктуаций физического вакуума, т.е. так называемых “нулевых колебаний” вакуума. На более простом классическом языке это можно выразить так: электроны подвержены воздействию случайных волн эфира, которые заставляют электроны “дрожать”, т.е. совершать своеобразное квазиброуновское движение в вакууме.

   В результате таких воздействий импульсы и координаты электронов изначально разбросаны случайным образом вблизи некоторых средних значений, измеряемых в экспериментах. По этой причине, например, невозможно все электроны при помощи кулоновского поля направить точно в центры атомных ядер. Выражаясь образным языком, можно сказать, что электрон всегда выступает в роли “плохого стрелка”. Подавляющее большинство электронов наверняка “промахнутся”, т.е. пройдут где-то вблизи ядер, но будут захвачены кулоновским полем ядер и продолжать случайное движение в окрестности этих ядер. Примерная картина такого движения для атома водорода представлена на рис.3.1.

   Поскольку минимальный фазовый объем  DW  для атомных масштабов достаточно велик, а размеры ядер очень малы, то лишь очень редким электронам удастся угодить в ядро, да и то, наверняка, не в “десятку”, поскольку вероятность такого события практически равна нулю.

  Из схемы движения электрона хорошо видно, что для центральных полей фазовый объем и орбитальный механический момент для отдельной траектории очень тесно связаны между собой.

   В силу полной сферической симметрии среднее значение орбитального механического момента электрона в основном состоянии атома равно нулю, чего нельзя сказать про среднеквадратичное значение этого же момента.

    Согласно теореме вириала для центрального кулоновского поля средние значения кинетической энергии  K  и потенциальной энергии  U  электрона связаны между собой следующим образом:

                   <K > = - <U >/ 2 .                                                       (2)

В декартовых координатах это выглядит так:

<p_x² + p_y² + p_z² > /2m = <e²/8 p e₀ (x ² + y ² + z ²) ^1/2 >.                              (3)

Для среднеквадратичных отклонений  Dx_ск  с учетом того, что в силу сферической симметрии <D p_x²> = <D p_y²> = <D p_z²> и  <D x ²> = <D y ²> =

 <D z ²> из соотношения (3) получаем

                   <D p_x²> D x_ск = A ,                                                                 (4)

где константой  А  обозначены все коэффициенты в (3).

   С другой стороны, согласно теореме Лиувилля минимально допустимый фазовый объем  DW = h  накладывает свои ограничения на величины  D x  и  D p_x

<D p_x ² > <D x ² >   ³  h ².                          (5)

 Подставляя значение  <D p_x ² >  из (5) в (4), получаем

                    <D x ² >/D x _ск  ³  A h ².                                        (6)

          Отсюда получаем

                                               D x _ск  ³  A h ².                         (7)

    Из неравенства (7) следует, что размеры атомов в среднем не могут быть меньше некоторой величины, определяемой минимально возможным фазовым объемом  DW = h. Поскольку произведение             D p_ск  D r_ск   определяет и механический момент электрона относительно ядра, то среднеквадратичное значение этого момента не может быть сколь угодно малой величиной, а должно быть порядка постоянной Планка  h.

   Поскольку в основном состоянии атома водорода электрон совершает под воздействием «нулевых» колебаний физического вакуума только случайное квазиброуновское движение вокруг ядра, средние значения момента количества движения и его проекций на некоторые выделенные оси обращаются в нуль. Такое состояние движения электрона в атоме называют  s-состоянием. Однако если такой атом поместить в магнитное поле, то у электрона может появиться ненулевая проекция механического момента на выделенную ось, которая может быть определена статистическими методами. Это будет рассмотрено в разделе о спине электрона в монографии [1].

ЛИТЕРАТУРА

1. Шаляпин А.Л., Стукалов В.И. Введение в классическую электродинамику и атомную физику. Второе издание, переработанное и дополненное. Екатеринбург, Изд-во  Учебно-метод. Центр УПИ, 2006, 490 с.

http://s1836.narod.ru  http://s1836.land.ru  

2. Поль Р.В. Оптика и атомная физика. М.: Наука, 1966. С. 475.

3. Ландау Л.Д., Лифшиц Е.М. Механика. – М.: Наука, 1968. Т. 1.

4. Рейф Ф. Берклеевский курс физики. Том 5. Статистическая физика. – М.: Наука, 1986. С. 122, 163, 208.